Skinned Multi-Person Linear Model (SMPL)

Realistic 3D model of the human body that is based on skinning and blend shapes

Figure 1: (left) SMPL model (orange) fit to ground truth 3D meshes (gray). Image and caption from

Introduction

In today’s rapidly evolving digital world, creating realistic and versatile human body representations is crucial for various applications, including animation, virtual reality, and video game development. If you’ve ever wondered how these lifelike 3D characters are brought to life, you’re in for a treat! In this blog post, we’ll dive into the fascinating world of the Skinned Multi-Person Linear (SMPL) body model—a cutting-edge approach to 3D human body modeling. Join me as we explore the inner workings of SMPL, learn how to harness its power through a step-by-step demo, and discover the potential applications that could revolutionize the way we interact with digital characters.

Skinned Multi-Person Linear Model (SMPL) is designed to create 3D models of human bodies, considering variations in body shape and posture. The different components of this model, such as the rest pose template, blend weights, and blend shapes A blend shape is a deformed version of a base 3D mesh (usually a character's face or body) that represents a specific shape or expression. By interpolating between the base mesh and one or more blend shapes, you can create smooth transitions between different expressions or poses., are learned from a large dataset of 3D scans of different people in various poses. One unique aspect of SMPL is that the pose-dependent blend shapes are based on a simple linear function of the pose rotation matrices, which makes it easier to train the model. The model specifically learn blend shapes to correct for the limitations of standard skinning. Different blend shapes for identity, pose, and soft-tissue dynamics are additively combined with a rest template before being transformed by blend skinning Blend skinning is a way to calculate how the vertices (points) of a 3D mesh should move when a character's joints (like an elbow or knee) rotate. It works by assigning weights to each vertex, which determine how much influence a nearby joint has on the vertex's movement. When a joint rotates, the vertices connected to that joint move according to their assigned weights, creating a smooth deformation of the character's mesh..

So why do we need these body models?

In animating realistic human bodies, the commercial approach is usually to hand rig the meshes and manually sculpt blend shapes. This approach takes a lot of manual work and hence large amount of time is needed to get the blend shapes right. So the research community has focused on learning a statistical body model from thousands of 3D body scans of real people in different shapes and poses.

Overview of the SMPL Body model

The SMPL body model uses the objective of minimizing the difference between the predicted 3D mesh and the ground truth 3D mesh. To capture how people’s bodies change with different poses, the researchers used 1,786 high-resolution 3D scans of various subjects in a wide range of poses. The model was trained to optimize various parameters, including blend weights, pose-dependent blend shapes, the mean template shape (rest pose), and a regressor that predicts joint locations based on body shape. This joint regressor is crucial for creating realistic pose-dependent deformations for any body shape, as it predicts joint locations as a function of body shape.

The model is trained on a large dataset of 3D scans of different people in various poses. The model is trained to learn the following components:

• Rest pose template The rest pose template is a 3D mesh of a human body in a neutral pose. It is the base mesh that is used to create the final 3D mesh.
• Blend weights The blend weights are the weights assigned to each vertex of the rest pose template. These weights determine how much influence a nearby joint has on the vertex's movement.
• Shape Blend shapes The shape blend shapes are the deformed versions of the rest pose template that represent a specific shape or expression.
• Pose-dependent blend shapes The pose-dependent blend shapes are the deformed versions of the rest pose template that represent a specific pose.
• Joint regressor The joint regressor is a linear regressor that predicts joint locations as a function of body shape.

Figure 2: (a) Template mesh with blend weights indicated by color and joints shown in white. (b) With identity driven blendshape contribution only; vertex and joint locations are linear in shape vector $ \color{green} \overrightarrow{\beta} $ (c) With the addition of pose blend shapes in preparation for the split pose; note the expansion of the hips. (d) Deformed vertices reposed by dual quaternion skinning for the split pose.Image and caption from

Figure 3: Summary of the SMPL body model with rest pose template, shape blend shapes, pose-dependent blend shapes and final mesh.

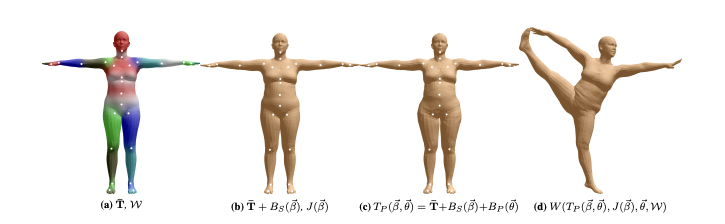
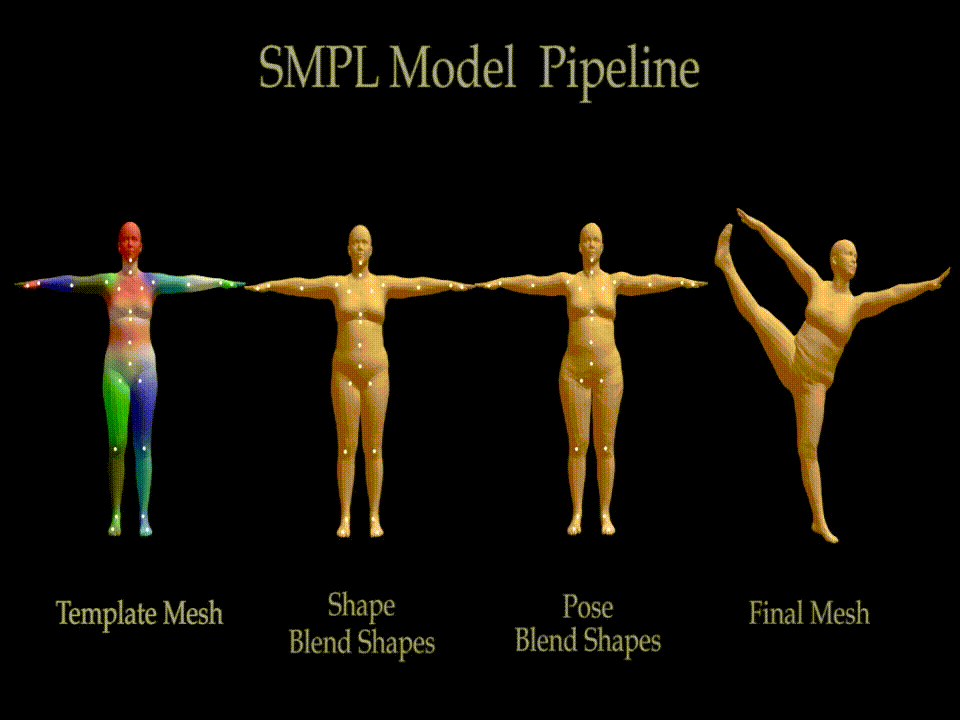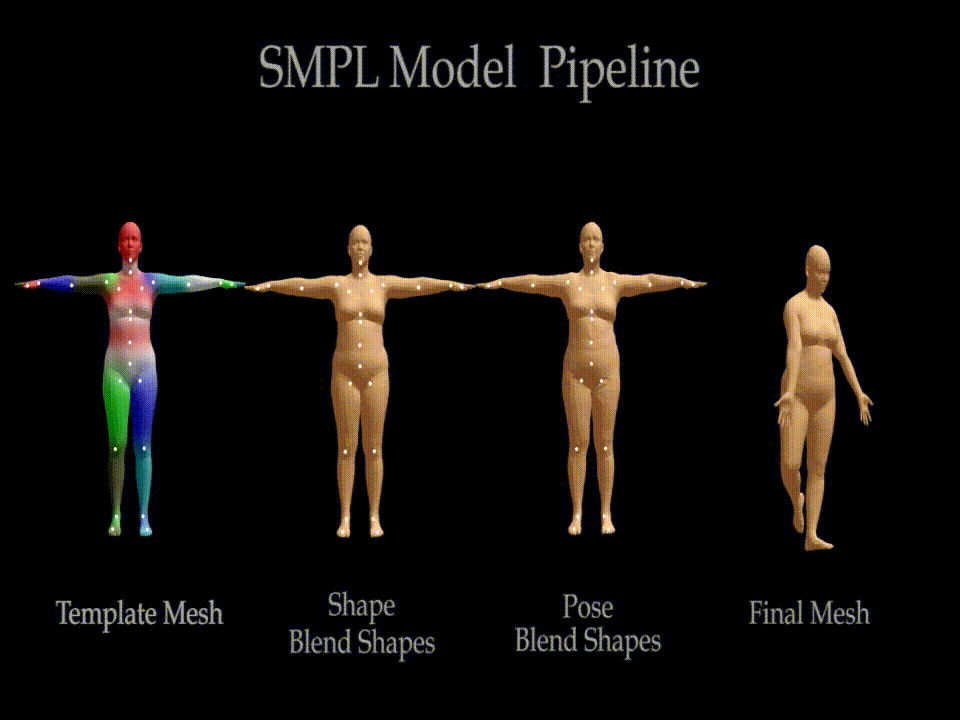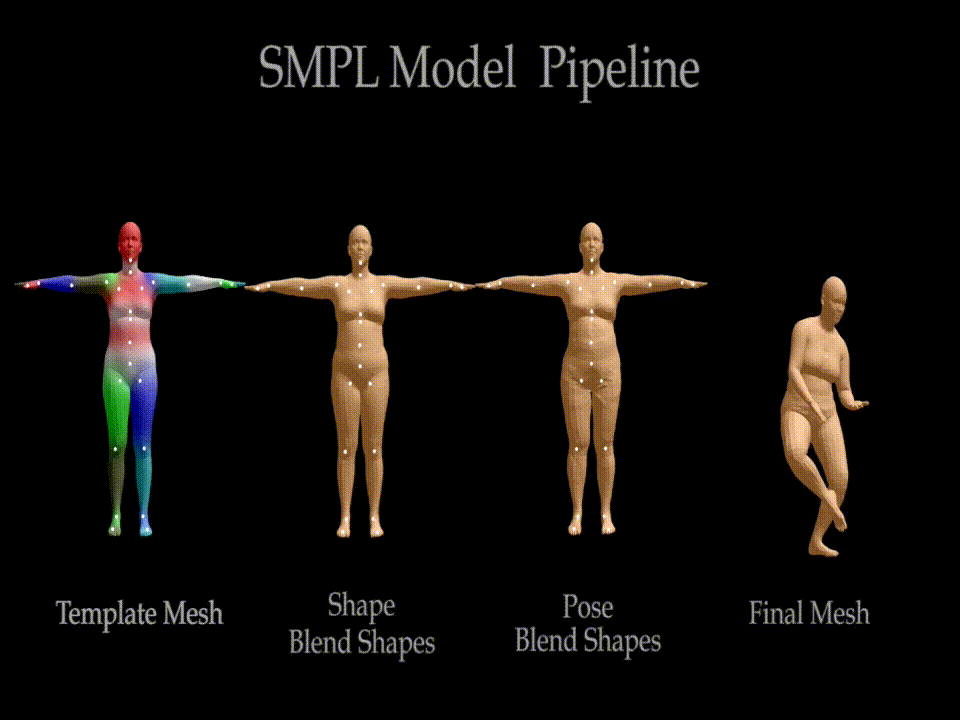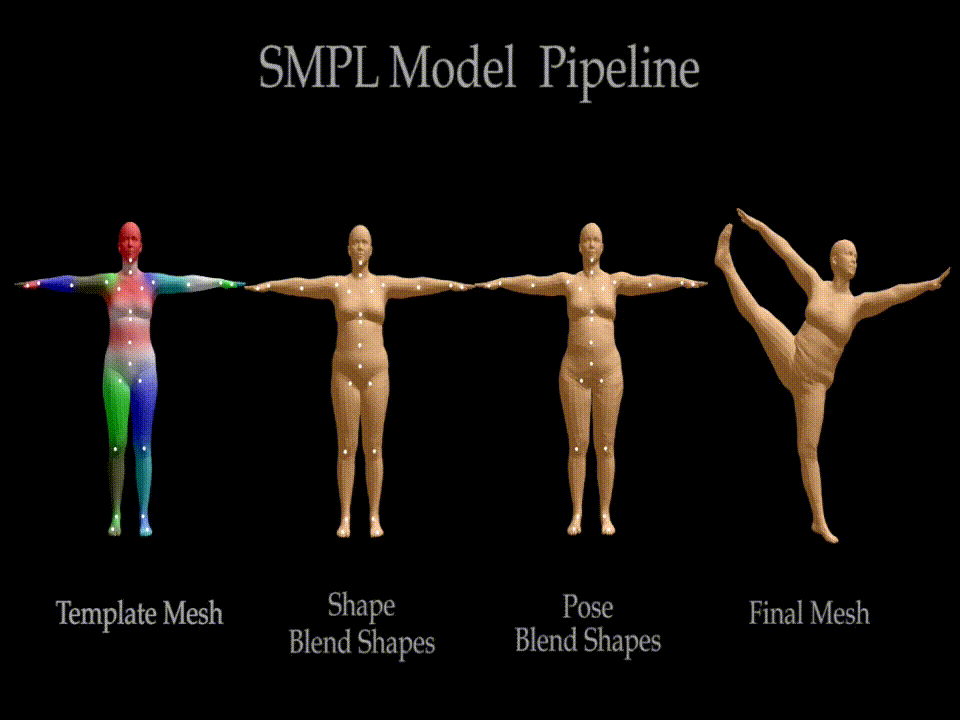
SMPL Model Formulation

The SMPL model is formulated as a linear combination of the rest pose template, shape blend shapes, and pose-dependent blend shapes. The final 3D mesh is obtained by adding the rest pose template and the pose-dependent blend shapes to the shape blend shapes, and then applying blend skinning to the resulting mesh. SMPL takes a vertex-based approach to skinning, which means that the vertices of the rest pose template are transformed by the joints of the skeleton. The weights of the vertices are determined by the distance between the vertices and the joints. The closer the vertices are to the joints, the higher the weight assigned to them. The weights are then used to calculate the final position of the vertices. A single blend shape is represented as created mesh with N=6890 vertices and K = 23 joints.

Following a standard skinning practice, the model is defined by :

• a mean template shape represented by a vector \(N\) concatenated vertices \(\bar{T} \in \mathbb{R}^{3N}\) in the zero pose \(\tilde{\boldsymbol{\theta}}^{*}\)
• \(W \in \mathbb{R}^{N \times K}\) :- a set of Blend Weights (Fig. 2(a))
• \(B_{S}(\tilde{\boldsymbol{\beta}}):\mathbb{R}^{\mid \tilde{\boldsymbol{\beta}}\mid} \rightarrow \mathbb{R}^{3N}\) :- a Blend Shape function that takes as input a vector of shape parameters, \(\tilde{\boldsymbol{\beta}}\), and outputs a blend shape sculpting the subject identity (Fig. 2(b))
• \(J(\tilde{\boldsymbol {\beta}}) : \mathbb{R}^{\mid \tilde{\boldsymbol{\beta}}\mid} \rightarrow w \mathbb{R}^{3K}\) :- a Joint Regressor function to predict \(K\) joint locations (white dots in Fig. 2(b)) as a function of shape parameters, \(\tilde{\boldsymbol{\beta}}\)
• \(B_{P}(\tilde{\boldsymbol{\theta}}) : \mathbb{R}^{\mid \tilde{\boldsymbol{\theta}}\mid } \rightarrow \mathbb{R}^{3N}\):- a Pose-Dependent Blend Shape function that takes as input a vector of pose parameters, \(\tilde{\boldsymbol{\theta}}\), and accounts for the effects of pose-dependent deformations (Fig. 2(c)).

The corrective blend shapes of these functions are added together in the rest pose as illustrated in (Fig. 2(c)). Finally, a standard blend skinning function \(W(\cdot)\) (linear or dual-quaternion) is applied to rotate the vertices around the estimated joint centers with smoothing defined by the blend weights. The result is a model, \(M(\tilde{\boldsymbol{\beta}}, \tilde{\boldsymbol{\theta}}; \boldsymbol{\Phi}) : \mathbb{R}^{\mid \tilde{\boldsymbol{\theta}}\mid \times \mid \tilde{\boldsymbol{\beta}}\mid} \rightarrow \mathbb{R}^{3N}\), that maps shape and pose parameters to vertices (Fig. 2(d)). Here $\boldsymbol{\Phi}$ represents the learned model parameters.$$